以下記錄我研究著名的 Floyd-Warshall 演算法自己整理的心得:
Floyd-Warshall Algorithm
1. 在All-Pairs Shortest Path的問題中,為了減低 DP 的時間複雜度,可使用Floyd-Warshall演算法。這種演算法,在edge weight為正或負時皆可實行。
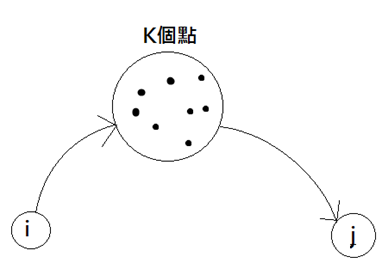
2. 假如要從 i 節點走到 j 節點,且中間有可能經過 k 個中間節點(intermediate vertex)。那麼從 i 到 j 的最短路徑長度等於(設中間節點數目不等於0):
min { (i 不經過第 k 個 intermediate vertex但有經過其他k-1個intermediate vertex 走到 j 的最短路徑) , (先到第 k 個intermdiate vertex 且經過其他 k-1個中間節點的最短路徑 + 由第 k 個點過 k-1 個 intermediate vertex 到達 j 的最短路徑) }
如圖所示:
整體而言就是決定是否要經過第 k 個點而已。如果經過第 k 個 intermediate vertex會讓總長度變小,那麼就選擇經過第 k 個點。如果 k = 0 當然最短路徑長就是 i 跟 j 之間的 weight。
3. predecessor matrix 裡存的是到達 j 點時, j 點的前一個 vertex 是誰。這又分為兩種情況,如果最短路徑是不經過第 k 點的,那麼predecessor matrix要檢查的區間就是 i~j 之間(經過k-1個intermediate vertex),反之有經過第 k 點,檢查區間為 k~j 之間(經過k-1個intermediate vertex)。