[演算法] heap sort

以下的心得，以Max-heap為例：
1.   max heap的特性：
      一個node的parent的索引值是這個node的索引值除以2之後取floor。一個node的左邊child是這個node索引值乘以2，右邊的child的索引值是當前node索引值乘以2之後再加上1。
     因此可以定義macro：
     #define Parent(i) i/2
     #define Left(i) 2*i
     #define Right(i) (2*i)+1
2.   以下方法，可以很快地寫出一個heap sort：
      首先迅速建立heap，要維持一個heap，只須有2個部分：
      第一部份，要有一個函式可以調整任意一個node往下樹的下方移動，使整個樹維持max heap的特性。做到這一點只要比較這個node跟其兩個child三者之中誰最大，將要調整的node與其child中最大的數值調換。如此將node往下調整移動後，再將剛剛調換過的child那個位置，傳入自己這個函式，遞迴呼叫自己，繼續從那個位置往下調整。
      第二部分，要建立一個heap，需要定義這個heap的大小，整個heap中有幾個node一定要知道。將整個陣列視為heap時：

   
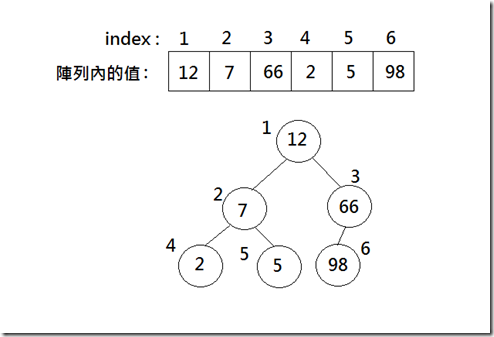
這樣子的排法， heap圖內的索引值，注意是從1開始算，在這種情況下，最大的索引值就是整個陣列的size。在建立heap時，要從索引值為 (size/2) 的那個node，開始往索引值小的node去將每個node檢查並往下調整，使整個tree有max-heap之特性。索引值大於size/2的那些node，通通都是樹葉(leaf)，樹葉不用調整。
由以上的觀念可以迅速建立heap。
3.   用heap來排序，就是heap sort。非常容易，只是將root取出，然後把最後一個node(最後一片樹葉)，摘下來貼到root的位置，然後從root往下調整，使整個heap維持max-heap的特性。注意此時要更新size的大小，將整個heap的size減1。